Definição de Função

Função é um dos conceitos mais importantes da matemática. Existem várias definições, dependendo da forma como são escolhidos os axiomas. Uma relação entre dois conjuntos, onde há uma relação entre cada um de seus elementos. Também pode ser uma lei que para cada valor x é correspondido por um elemento y, também denotado por ƒ(x). Existem inúmeros tipos de funções matemáticas, entre as principais temos: função sobrejetora, função injetora, função bijetora, função trigonométrica, função linear, função modular, função quadrática, função exponencial, função logarítmica, função polinomial, dentre inúmeras outras. Cada função é definida por leis generalizadas e propriedades específicas


Nome: Vanessa Nascimento Rolim Nunes
Numero: 45
Curso : Aquicultura

ultilidades dos triangulos retangulos no dia a dia

Razões para estudar triângulos Retângulos

		INTRODUÇÃO
		Como medir a altura de um arranha-céu de 100 andares sem escalá-lo? Ou medir a largura de um rio sem atravessá-lo de uma margem à outra?   A trigonometria é o ramo da matemática que trata das relações entre os lados e ângulos de triângulos e serve para calcular distâncias inacessíveis, muito utilizadas na astronomia e geografia. A trigonometria é uma ferramenta da  Engenharia, Arquitetura, Física, Aeronáutica, Navegação, Topografia e em toda atividade que envolve a localização espacial de pontos e o cálculo de distâncias entre eles. Enfim, a trigonometria serve para uma infinidade de cálculos, dentre eles, podemos citar: calcular a quantidade de degraus necessários para por numa escada, determinar o tamanho e declividade de um terreno para evitar deslizamentos e assim salvar vidas, calcular o ângulo certo para lançamento de misses e foguetes, calcular o ângulo de declividade de rampas de acessos a prédios e etc. Nesta Situação de aprendizagem vamos estudar as razões trigonométricas. As ideias fundamentais referentes às razões trigonométricas serão apresentadas buscando-se uma articulação com o que já foi estudado em séries anteriores. Exemplos ilustrativos servirão para a contextualização e a articulação do conteúdo Nome: Vanessa Nascimento e Dara Rute  Numero: 45 e 14  Curso: AQUICULTURA

SOH CAH TOA - VÍDEO-AULA

Vanessa Nunes Nascimento

Aquicultura 1° C

N°- 45

Funções e não Funções

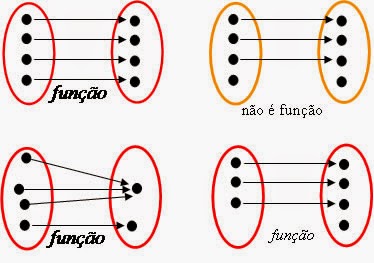
•  Verifique quais dos diagramas representam função de A= {3,4,5} em B= {2,3,4} .Justifique sua resposta 

RESPOSTA=

 a) É uma função pois cada elemento de A tem um único correspondente em B .

b) É uma função pois cada elemento de A tem um único correspondente em B

RESPOSTA=

c) Não é função pois existe um elemento de A (5) que não tem correspondente em B .

d) Não é função pois existe um elemento de A (3) que tem dois correspondentes em B .

Nome:Vanessa Nascimento Rolim Nunes 

Numero: 45 

Curso: Aquicultura

Não é função pois o dominio de x não pode pertence a dois contra dominios de y.

Vanessa Nunes
Aquicultura
1º-c
nº 45

Exercicios Sobre Função

EXERCICIOS

1)       Obtenha a lei das funções de 1º grau que passam pelos pares de pontos abaixo:

a)       (-1, 2) e (2, -1)             b)  (-1, 0) e (3, 2)

2)       Determine a lei da função do 1º grau cujo gráfico intercepta os eixos coordenados nos pontos (2, 0) e (0, 3).

3)       Determine a lei da função do 1º grau cujo gráfico passa pelo ponto (2, 3) e cujo coeficiente linear vale 5.

4)       Dada a função y = 3x – 2, calcule os valores de x que tornam a função negativa.

5)       Dada a função y = –2x + 1, calcule os valores de x que tornam a função positiva.

 Olá galera exercita é sempre bom , tente resolver este aqui.

Vanessa Nunes 

Aquicultura

1º-C

Sejam A={2,4,6,8}, B={1,3,5,7} e a relação R em A×B apresentada pelo seu gráfico cartesiano.


Identifique se cada afirmação é V (verdadeira) ou F (falsa).

a. (2,1) pertence à relação R.
b. (3,2) pertence à relação R.
c. (4,3) pertence à relação R.
d. (5,6) pertence à relação R.
e. (8,7) pertence à relação R.

 A=VERDADEIRA
 B=FALSA
 C=VERDADEIRA
 D=FALSA
 E=VERDADEIRA
  
NOME=DARA RUTE
N=14
 
http://pessoal.sercomtel.com.br/matematica/medio/funcoes/funcoes-a.htm

     Qual dos gráficos representa uma função sobrejetora?






RESPOSTA=A

NOME=TAISA EDUARDA
N=42


http://pessoal.sercomtel.com.br/matematica/medio/funcoes/funcoes-a.htm

Imagens de Plano Cartesiano

 

Nome: Vanessa Nascimento 

Numero: 45 

Curso: Aquicultura 1 

1. Qual é o coeficiente linear da função f(x) = 2x - 1?
   
   • - 2
     
   • - 1
     
   • 1
     
   • 2
     R= -1
     
     NOME=TAISA EDUARDA
     N=42
     
      http://rachacuca.com.br/quiz/82222/exercicios-de-funcoes-do-1o-grau/
     

1. Uma função f estabelece uma relação entre dois conjuntos X e Y, por exemplo, de maneira que a função f de X em Y que relaciona cada elemento x em X a um único elemento y = f (x) em Y. Essa afirmação é verdadeira ou falsa?
   • Verdadeira
     
   • Falsa
     

R=VERDADEIRA

NOME=TAISA EDUARDA
N=42
CURSO=AQUICULTURA "1"

http://rachacuca.com.br/quiz/82222/exercicios-de-funcoes-do-1o-grau/

 http://exercicios.brasilescola.com/matematica/exercicios-sobre-funcoes.htm#resposta-2128

Em uma indústria metalúrgica o custo de produção de uma peça automotiva corresponde a um custo fixo mensal de R$ 5 000,00 acrescido de um custo variável de R$ 55,00 por unidade produzida mais 25% de impostos sobre o custo variável. Considerando que o preço de venda dessa peça pela indústria aos comerciantes é de R$ 102,00, determine:

a) a função custo da produção de x peças.
b) a função receita referente a venda de x peças.
c) a função lucro na venda de x peças.
d) o lucro obtido com a venda de 500 unidades.

RESPOSTA

a) A função custo será dada pela somatória do custo fixo, do custo variável e do imposto cobrado de acordo com o custo variável.
Custo = 5000 + 55x + 0,25 * 55x
b) A função receita é dada por:
Receita = 102x
c) A função lucro é obtida subtraindo a função receita da função custo.
Lucro = 102x – (5000 + 55x + 0,25 * 55x)
Lucro = 102x – 5000 – 55x – 0,25 * 55x
Lucro = 102x – 55x – 13,75x – 5000
Lucro = 33,25x – 5000
Quando calculamos a função lucro determinamos uma expressão capaz de determinar o lucro líquido obtido da venda de x peças, isto descontados os custos de produção e os impostos municipais, estaduais e federais.
d) O lucro obtido com a venda de 500 unidades corresponde a:
f(x) = 33,25x – 5000
f(500) = 33,25 * 500 – 5000
f(500) = 16 625 – 5000
f(500) = 11 625
O lucro obtido é igual a R$ 11 625,00.















NOME=TAÍSA EDUARDA ANDRDADE DA SILVA
N=42
CURSO=AQUICULTURA "1"

Observe na tabela o numero de locações de DVDs realizadas por uma locadora e o preço total correspondente

A)-O preço da locação e dado em função de que?
R=Quanto mais locação, maior o valor

B) Escreva uma lei matemática que associe o numero X de locações com o preço Y
 R=   1         5                                       (Y = 5X)
         2         10
         3         15
         4         20

C) Qual é o preço de 20 locações de DVDs?
R= 20.5=100

ALUNA= TAISA EDUARDA
N= 42
CURSO= AQUICULTUIRA 1

Funções

Nome: Vanessa Nascimento Rolim Nunes 

Numero: 45 

Curso: Aquicultura

Plano Cartesiano

1º Quadrante tem X maior ou igual e Y maior ou igual 

2º Quadrante tem X menor ou igual e Y menor ou igual 

3º Quadrante tem X menor ou igual e Y maior ou igual 

4º Quadrante tem X maior ou igual e Y menor ou igual  

Nome: Vanessa Nascimento 

Numero: 45 

Curso: Aquicultura 1

Conjuntos de A , B e IM (F)

O conjunto de A tem um único correspondente do conjunto B por isso é uma função .

Conjunto A - Domínio da função 

Conjunto B - Contradomínio de A 

Imagem da Função - Todos os valores de Y



Nome: Vanessa Nascimento
Numero: 45
Curso: Aquicultura

Definição de Função

FUNÇÃO =  É a relação entre duas grandezas tal que uma corresponde a um único valor da segunda . 
  


Nome: Vanessa Nascimento
Numero: 45 
Curso: Aquicultura 1 

http://www.matematicadidatica.com.br/PlanoCartesiano.aspx

O Plano Cartesiano foi criado pelo matemático René Descartes. Como ele associava a geometria à álgebra, esta foi a forma que ele criou para representar graficamente expressões algébricas

.

A sua utilização mais simples é a de representarmos graficamente a localização de pontos em um determinado plano. Através dele também podemos representar um segmento de reta ou um triângulo, por exemplo.

O plano cartesiano é composto de duas retas perpendiculares e orientadas, uma horizontal e outra vertical.

Damos no nome de eixo x ou eixo das abscissas à reta horizontal. À vertical denominamos de eixo y ou eixo das ordenadas

ALUNA=TAISA EDUARDA ANDRADE DA SILVA
N= 42

01- Dados os conjuntos A={a,b,c} e B={1,2,3,4}, podemos construir a relação R em A×B que está apresentada no gráfico.

Qual resposta mostra a relação R de forma explicita?

a. R={(a,1),(b,3),(c,4),(a,3)}
b. R={(1,a),(4,a),(3,b),(c,2)}
c. R={(a,1),(b,3),(c,2)}
d. R={(a,1),(a,4),(b,3),(c,2)} 

(a) Não, pois a relação deve conter (c,2) e (a,4).
(b) Não, pois os elementos da esquerda devem estar relacionados com os da direita, e não o contrário.
(c) Não, pois falta o par ordenado (a,4).
(d) Resposta correta.

ALUNNA= TAISA EDUARDA ANDRADE DA SILVA

N= 42 

http://pessoal.sercomtel.com.br/matematica/medio/funcoes/funcoes-a.htm